This article will unravel the essentials of algebra, a subject that often intimidates beginners. But, with a clear understanding, I can assure you that algebra is not as complex as it might seem at first glance. Think of algebra as a tool that allows us to solve puzzles where some pieces, the unknown numbers, are missing. The beauty of algebra lies in its universality; it serves as a language by which we can articulate and solve an array of problems.

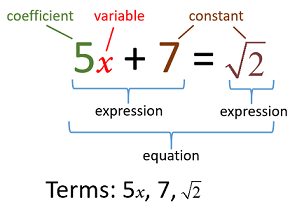
At its core, algebra uses variables, represented by letters, to stand in for these unknown values. Imagine you’re cooking but are missing a couple of ingredients from the recipe. In algebra, these ingredients are like ‘x‘, ‘y‘, or ‘z‘. They are placeholders waiting to be discovered. Variables when combined with known values, the constants like 2, -7, or 0.068, create expressions that model real-life scenarios.

So, what is a constant? It’s simply the part of the equation that doesn’t change. In algebra, constants and variables work together like a dance duo, each playing a crucial role. Constants ground the variables, helping us understand the framework within which we’re working.

Algebra isn’t just a set of abstract concepts; it’s a powerful tool used to articulate and solve real-world problems. From calculating the trajectory of a spacecraft to devising a budget plan, algebra makes it all possible.

Having laid the groundwork, it’s important to understand the specific rules and properties that allow us to manipulate algebraic expressions effectively. Knowing these rules is like having a roadmap that guides us through the maze of mathematical problem-solving.

NAVIGATING THE RULES AND PROPERTIES OF ALGEBRA

The principles that turn the wheels of algebra are processes that might seem abstract at first glance, but are actually deeply rooted in logic and application. The commutative and associative properties aren’t just mathematical jargon; they’re the backstage crew that ensures every algebraic performance runs smoothly. Whether you’re rearranging equations or simplifying expressions, these rules are your trusty guide.

Take the commutative properties of addition and multiplication. When you see ‘a + b = b + a‘ or ‘a × b = b × a‘, remember, the order in which you add or multiply numbers doesn’t affect the result. This might seem like a small detail, but it’s a powerful tool that often simplifies complex problems.

Now think about the associative properties. These tell us that it’s not just the final destination that matters – it’s also the route we take. By regrouping numbers, ‘a + (b + c) = (a + b) + c‘ and ‘a × (b × c) = (a × b) × c‘, we gain the flexibility to tackle larger problems with greater ease.

In a nutshell, the rules and properties of algebra are your roadmap to success. They give you the freedom to maneuver within the realm of numbers with confidence. Whether you’re solving for ‘x‘ in a classroom or calculating a budget, algebra lays the groundwork for a strong mathematical foundation. And with this foundation, you’re equipped to solve not just mathematical puzzles, but real-world challenges as well.