Sets are fundamental in mathematics, and getting a good grasp on them can really help with a bunch of other topics. A set is simply a collection of items or numbers. The items in a set are called elements.

Set notation is a way to describe these collections clearly. For example, when you see A = {…}, it means A is a set containing certain elements. If you see X ∈ A, it means that X is an element of A. On the flip side, if you see Y ∉ A, it means Y is not an element of A.

Now, you might come across the notation n(A), which just tells you the number of elements in set A. This way of writing things makes mathematical communication clear and precise.

There are times when sets are defined using algebra. For instance, A = {x : x + 2 < 5>

VENN DIAGRAMS

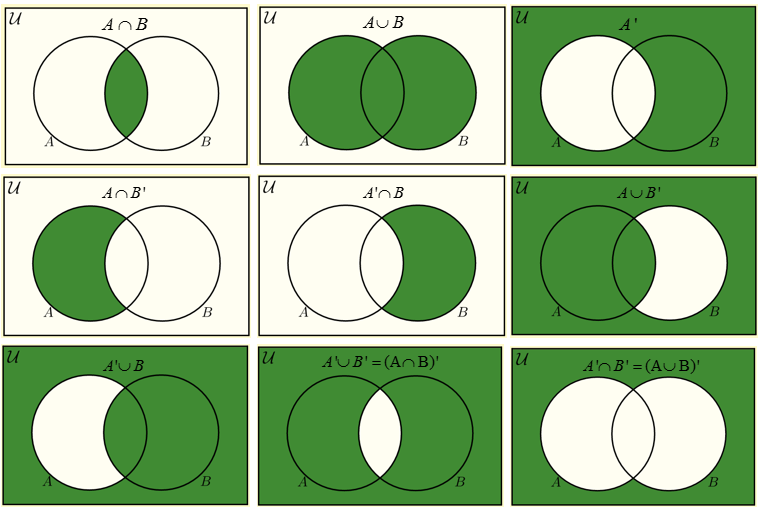
Venn diagrams are super handy tools for visualizing sets and their relationships. They use circles to represent sets, helping you see when sets overlap or are separate. Each circle in the diagram represents a set, and the areas where circles overlap represent the elements that the sets have in common.

Practicing with Venn diagrams will strengthen your understanding of sets and help you interpret complex problems. Use them to break down problems into manageable parts, and you’ll find that solutions come more easily. Keep at it, and these diagrams will become a go-to tool in your maths toolkit.

UNIONS AND INTERSECTIONS

These diagrams are not just for show. They’re practical for solving problems, especially those involving the number of elements in sets. For example, if you’re given sets A and B, their intersection (A ∩ B) includes elements that are in both sets, while their union (A ∪ B) includes elements that are either in A, B, or both.

Imagine a Venn diagram with two overlapping circles. One represents students who like mathematics (set A), and the other represents students who like science (set B). The overlapping area (A ∩ B) shows students who like both subjects. By using this visual tool, you can easily answer questions about these groups of students, like how many like only one subject or both.

COMPLEMENT OF A SET

Venn diagrams also come in handy when dealing with the complement of a set. The complement, written as A’, is made up of all the elements in the universal set ξ that aren’t in set A. It’s an effective visual way to see what’s included and what’s excluded from a certain set.

CONCLUSION

Understanding these basics of sets and how they are notated is really important for moving forward in GCSE Maths. Not only do these concepts show up in exams, but they’re also foundational for more advanced topics. So, take the time to get comfortable with this language and practice writing out sets on your own.