Ratios are essential in comparing different quantities. When you see a ratio, it’s simply a way to show how much of one thing there is compared to another. For example, if you have a recipe that calls for 2 cups of flour and 1 cup of sugar, the ratio of flour to sugar is 2:1. This means there are two parts flour for every one part sugar.

RESOURCES

• Ratios: Volume 6 (Easy Steps Math) (https://amzn.to/420QV0o)
• Ratio Skills for Edexcel GCSE 9-1 Maths Higher (GCSE Topics) (https://amzn.to/3W5O6HV)

These are affiliate links. If you click a link and buy the product, then the blogger gets a percentage of the sale or some other type of compensation. Prices are not different if you use these affiliate links. You will not pay more by clicking through to a link.

SIMPLIFYING RATIOS

Simplifying ratios is a bit like reducing fractions. You divide both sides of the ratio by their greatest common factor. For instance, the ratio 8:4 can be simplified to 2:1 because both numbers can be divided by 4. This step helps make the ratios easier to understand and work with in more complex problems.

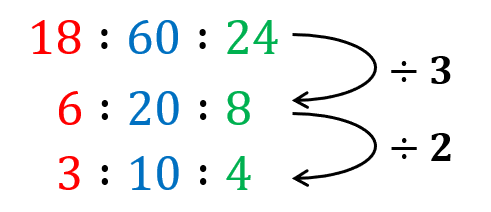
DIVIDING IN A GIVEN RATIO

Ratios aren’t just for simple comparisons – they play a crucial role in dividing quantities too. Suppose you have 80 candies to distribute between two friends in the ratio of 3:5. This means Friend A gets three parts and Friend B gets five parts. First, you add the ratio numbers together (3 + 5 = 8) to find the total parts. Then, you divide the total quantity (80 candies) by the total parts (8), which gives you 10 candies per part. Friend A gets 3 parts (3 x 10 = 30 candies) and Friend B gets 5 parts (5 x 10 = 50 candies).

CONCLUSION

In your day-to-day life, you could use ratios to work out everything from mixing paint colors to scaling a recipe. Imagine you need to prepare food for a larger group but want to keep the same taste. Knowing how to adjust the ratio of ingredients ensures everyone gets the same quality meal.

One common mistake people make is mixing up the order of the numbers in a ratio. To avoid confusion, always maintain the order given or required in the problem. Another pitfall is forgetting to simplify ratios, which can make calculations trickier than needed. Remember, simplifying makes it easier to see the relationship between quantities at a glance.