Percentages play a big part in everyday life. Whether you’re figuring out how much to tip at a restaurant, looking at discounts when shopping, or even keeping track of exam scores, percentages are everywhere. The term ‘per cent’ means ‘out of 100’. Essentially, when you write something as a percentage, you’re expressing it as a portion of 100.
For example, finding 50% of an amount is like dividing it in half. So, if you have £100, 50% would be £50. It’s the same for other common percentages. Finding 25% is like dividing by four; finding 10% is like dividing by ten. These tricks are quick and useful, especially when a calculator isn’t handy.
If you need to find a percentage of an amount, change the percentage to a decimal first. For instance, 20% becomes 0.20. Then, multiply this decimal by the amount you’re working with. If you have £200 and need to find 20%, you’d do 200 x 0.20 = £40.
Let’s put this into practice: How much is 30% of £150? First, change 30% to a decimal (0.30), then multiply it by £150. So, 150 x 0.30 = £45. Easy, right? Practicing these conversions helps to ensure that you’re comfortable, whether in a test or just managing your money day-to-day.
RESOURCES
These are affiliate links. If you click a link and buy the product, then the blogger gets a percentage of the sale or some other type of compensation. Prices are not different if you use these affiliate links. You will not pay more by clicking through to a link.
PERCENTAGES, FRACTIONS AND DECIMALS
Switching between percentages, fractions, and decimals can make problem-solving much easier. To convert a fraction to a decimal, divide the top number by the bottom number. To get a percentage from a decimal, multiply it by 100. For example, converting 1/4 to a decimal gives 0.25, and multiplying 0.25 by 100 gives you 25%. On the flip side, if you have a percentage like 75%, dividing by 100 converts it to 0.75.

PERCENTAGE INCREASE AND DECREASE
Increasing or decreasing an amount by a percentage is a common task. To increase an amount, calculate the percentage and then add it to the original figure. For example, if you want to increase £200 by 15%, find 15% of £200, which is £30, and add it to get £230. To decrease an amount, subtract the percentage from the original figure. If decreasing £200 by 15%, you subtract £30, leaving you with £170.

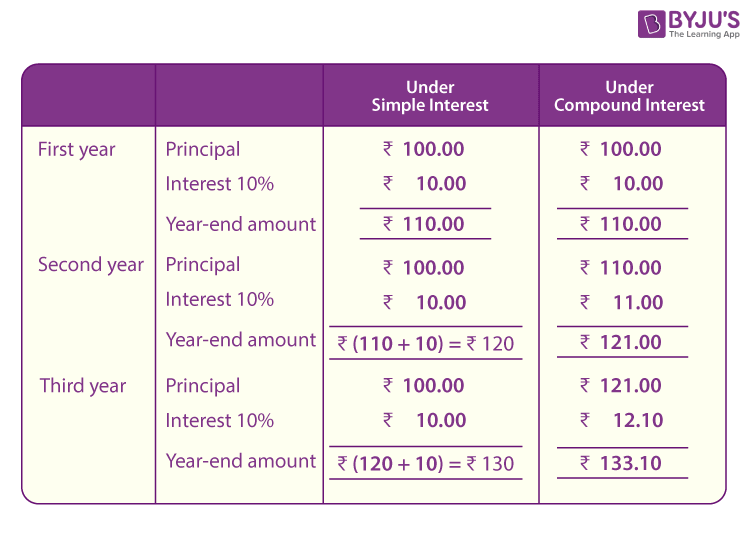
COMPOUND PERCENTAGE CHANGE
Compound percentage changes might sound tricky, but they follow a straightforward pattern. Compound interest, for example, involves adding interest to an initial sum over multiple periods. The following formula is handy:
Pn = Po x (1 + r/100)n
Here, Po is the initial amount, r is the percentage rate, n is the number of periods, and Pn is the amount after n periods. So, if you invest £1,000 at an annual interest rate of 5% for 3 years, your total will be:
£1,000 x (1 + 5/100)3 = £1,157.63
Compound decay works similarly but in reverse. It’s used when an amount decreases by a certain percentage over time, like with depreciation. The following formula is used:
Pn = Po x (1 – r/100)n
If a car worth £15,000 depreciates by 10% annually, after 2 years, it will be worth:
£15,000 x (1 – 10/100)2 = £12,150
CONCLUSION
Understanding how these advanced percentage concepts work can really give you an edge. They’re not just useful for exams but also for everyday financial decisions. Practice regularly, and soon calculating any percentage will be second nature.



No responses yet