RESOURCES
These are affiliate links. If you click a link and buy the product, then the blogger gets a percentage of the sale or some other type of compensation. Prices are not different if you use these affiliate links. You will not pay more by clicking through to a link.
EQUIVALENT FRACTIONS
Equivalent fractions are all about understanding that different fractions can represent the same value. Take the fraction ½; if you multiply both the numerator and the denominator by 2, you get ²⁄₄, which still represents the same value. This is where the beauty of fractions shines. By multiplying or dividing both the top and bottom numbers by the same thing, you can find as many equivalent fractions as you like. It’s important because it allows flexibility in solving many mathematical problems.
To simplify a fraction, you need to find its equivalent form using the smallest numbers possible. This is also called expressing a fraction in its lowest terms. For example, the fraction ⁸⁄₁₂ can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 4. So, ⁸⁄₁₂ becomes ⅔.

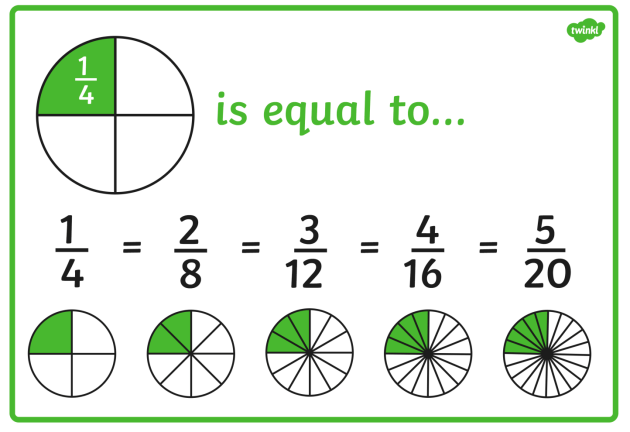
MIXED NUMBERS AND IMPROPER FRACTIONS
Mixed numbers combine whole numbers with fractions. Imagine having 1 whole pizza and half another one, you’d write it as 1½. This is simpler to understand than the improper fraction ³⁄₂, which means the same thing but isn’t as straightforward. Converting between mixed numbers and improper fractions is a useful skill, especially when you need to perform operations like addition and subtraction.
Improper fractions have numerators larger than their denominators. They look a bit intimidating at first, but they’re just another way of expressing numbers greater than one. When you know how to juggle between mixed numbers and improper fractions, things get easier. You can quickly convert ⁵⁄₃ to 1⅔ by dividing 5 by 3, and recognizing the remainder as the new numerator over the original denominator.


ORDERING FRACTIONS
Ordering fractions requires a common denominator. If you need to put ⅓ and ¼ in order, convert them so they have the same denominator, like 12. So, ⅓ becomes ⁴⁄₁₂ and ¼ becomes ³⁄₁₂. Now it’s clear which is bigger.

ADDING AND SUBTRACTING FRACTIONS
When adding or subtracting fractions, they need a common denominator. For example, to add ⅖ and ½, convert them to ⁴⁄₁₀ and ⁵⁄₁₀, making it simple to add them to get ⁹⁄₁₀. The same rule applies to subtracting fractions.

MULTIPLYING AND DIVIDING FRACTIONS
Multiplying whole numbers by fractions involves multiplying just the numerator and then dividing by the denominator. If you’re multiplying 3 by ⅖, multiply 3 by 2 to get 6, then divide 6 by 5 to get 1⅕. When dealing with two fractions, multiply the numerators together and the denominators together. For instance, ½ multiplied by ¾ is ⅜.
Dividing fractions uses the concept of reciprocals. If you want to divide ¾ by ½, flip ½ to get its reciprocal, ²⁄₁. Then multiply ¾ by ²⁄₁ to get ³⁄₂ or 1½. This method works every time.

FRACTIONS AND DECIMALS
Converting fractions to decimals bridges the gap between these two forms of numbers. For fractions like ½ or ¾, dividing the numerator by the denominator using a calculator or pencil and paper gives 0.5 and 0.75 respectively. This makes them easier to use in different contexts.
Terminating decimals stop after a few digits, like 0.25 or 0.5. Recurring decimals have a pattern that repeats endlessly. For instance, ⅓ as a decimal is 0.333… with the 3 repeating forever. Recognizing this can help convert decimals back to fractions. Writing 0.333… as ⅓ makes it clearer in many problems.
Practical conversion helps too. Knowing that ⅒ is 0.1 or ¹⁄₁₀₀ is 0.01 can speed up both arithmetic and understanding. These small steps often make solving complex problems easier.



No responses yet