DIRECT PROPORTION

Direct proportion means two quantities increase or decrease at the same rate. Imagine it as two friends who always walk side-by-side. When one takes a step, the other does too. The official way to say this is that p is proportional to l. It can also be said as p varies directly as l or just p varies as l.

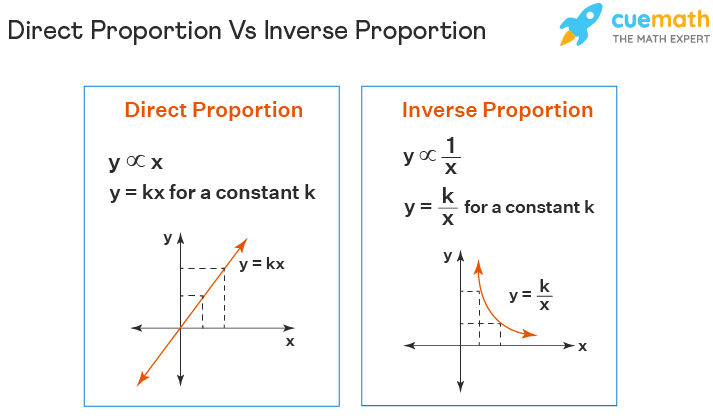
In terms of equations, this is written as p = kl. Here, k is the constant of proportionality. Think of k as the secret ingredient keeping the ratio between p and l consistent. If you graph this relationship, you’d get a straight line going through the origin. The slope of the line? That’s your k.

There are more complex forms of direct proportion too. For example, if a is directly proportional to the square of u, then the formula is a = ku². If a is directly proportional to the cube of u, it’s a = ku³. If h is directly proportional to the square root of g, you’ll write it as h = k√g. Different scenarios, but the concept remains the same.

Now let’s look at where you might actually see direct proportion in real life. Cooking is an excellent example. Double the ingredients, and you make double the servings. If you’re driving a car at a constant speed, the distance you cover is directly proportional to the time you drive. Leave the car for twice as long, and you go twice as far.

Understanding direct proportion helps in making predictions and understanding relationships between different quantities. Whether it’s in physics, economics, or everyday tasks, recognizing these patterns makes problem-solving much easier.

INVERSE PROPORTION

Inverse proportion is when one quantity increases, the other one decreases. Think of it like a seesaw. When one side goes up, the other must go down. The formal way to say this is that y is inversely proportional to x or y varies inversely as x.

In equations, inverse proportion is written as y = k/x, where k is the constant of proportionality. Here, k keeps the product of the two quantities constant. Graphing this relationship gives us a curve that gets closer to the axes but never touches them, also known as a hyperbola.

You’ll find variations of inverse proportion too. If a is inversely proportional to the square of u, the formula looks like this: a = k/u². If a is inversely proportional to the cube of u, it’s written as a = k/u³. If h is inversely proportional to the square root of g, it’s h = k/√g. Different formulas, same underlying principle.

So, where do you see inverse proportion in real life? Take speed and travel time, for instance. If you increase your speed, the time it takes to cover a certain distance decreases. Another example is in economics: if supply increases, the price often decreases, assuming demand stays constant.

Inverse proportions are everywhere, and understanding them helps in fields like engineering, finance, and science. Recognizing these relationships helps you make smarter decisions and understand how different variables interact with each other.