CIRCLE GRAPHS

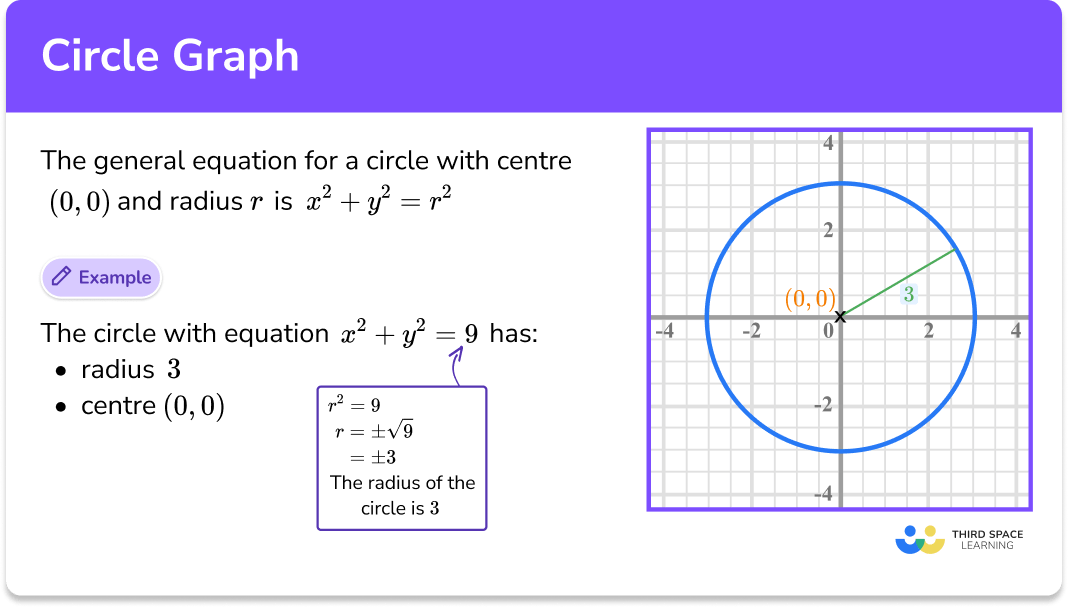
The equation of a circle is central to understanding circle graphs. This equation, (x – a)² + (y – b)² = r², represents a circle with radius r and center (a, b). It’s crucial to recognize this pattern as it frequently appears in various mathematical problems. By familiarizing yourself with plotting and interpreting this equation, you’ll be better equipped to handle more complex concepts involving circles.

TRIGONOMETRIC GRAPHS

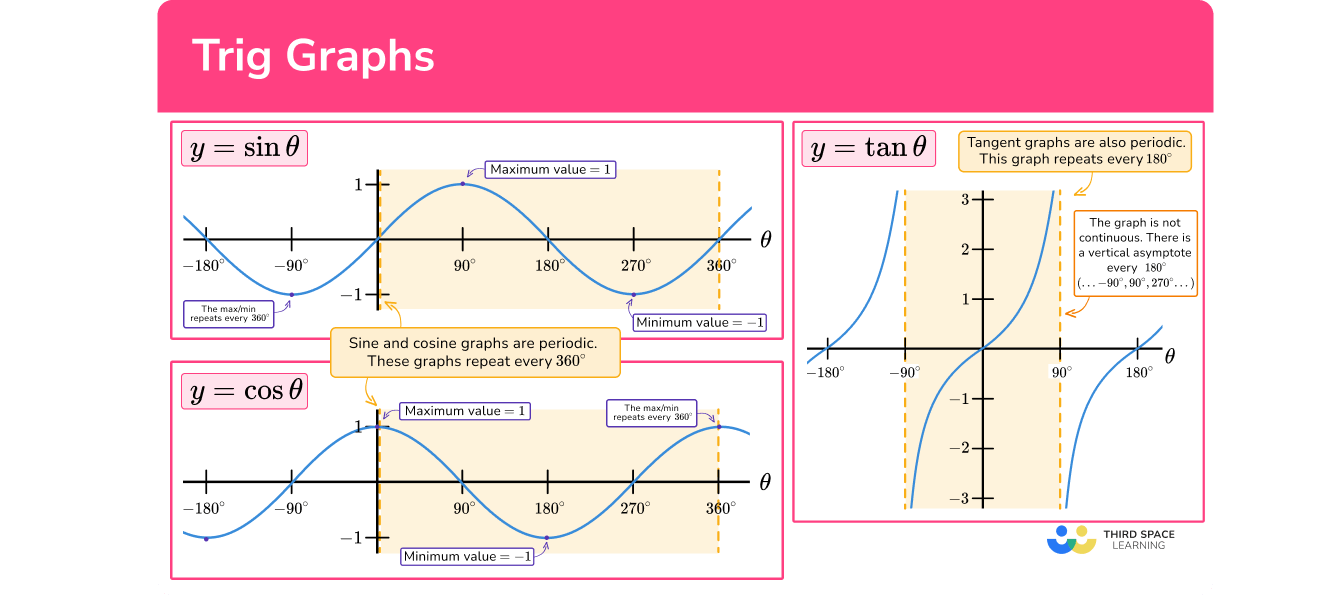
Moving to trigonometric graphs, the sine, cosine, and tangent functions are key players. These functions are periodic, meaning they repeat their values in a regular pattern. Sine and cosine functions have smooth, wave-shaped graphs and take values between -1 and 1. Both of these functions repeat every 360 degrees, which makes them predictable and easier to work with once you understand their cycles. Tangent, on the other hand, has a different characteristic: its graph repeats every 180 degrees and includes asymptotes at -90 and 90 degrees, points where the function is undefined. Recognizing these patterns can significantly aid in solving trigonometric problems.

TRANSFORMING GRAPHS

Transforming graphs involves changing their position or orientation on the coordinate grid. When a graph undergoes translation, it shifts but retains its shape. For example, if y = f(x) is your original graph, translating it up by a units results in y = f(x) + a, while translating it to the right by a units results in y = f(x – a).

In addition to translations, graphs can also be reflected across the x-axis or y-axis. A reflection in the x-axis changes the sign of the function’s output, represented as y = -f(x), while a reflection in the y-axis changes the sign of the input, shown as y = f(-x). Understanding these transformations allows you to manipulate and predict the behavior of functions more easily, enabling you to solve a broader range of mathematical problems. Points that do not move during these transformations are known as invariant points, and recognizing these can provide further insights into the nature of the graph.

CONCLUSION

Mastering the basics of circle, trigonometric, and transforming graphs can provide a solid foundation for understanding more advanced mathematical concepts. These three types of graphs are essential tools for visualizing and solving a range of problems in mathematics. Starting with the basics can simplify complex topics, making them more accessible and easier to grasp.