Circle geometry terms can sometimes seem complicated, but once you get the hang of the terms and their meanings, everything starts to fall into place. At its core, a circle is a simple shape: all points are the same distance from the center. This distance is known as the radius.
The circumference is the distance around the outside of the circle. Think of it like the perimeter of a circle—if you could take a circle and unwrap it, you’d have a straight line equal to the circumference.
The radius is essential because it’s half the diameter. That’s straightforward math—just double the radius and you’ve got the diameter. Drawing from this, the diameter spans from one edge of the circle, straight through the center, to the other side.
Next up is the tangent, which is a straight line that touches the edge of the circle at just one point. It doesn’t cut across the circle; it merely grazes it.
Now, let’s look at the arc. The arc is part of the circumference, sort of like a curved line segment. If you were to pick any two points on the edge of a circle, the arc would be the curved line connecting them.
A chord, on the other hand, is a straight line between two points on the circle. It may or may not pass through the center.
When you hear the term ‘sector,’ think of a slice of pie. It’s an area bound by two radii and the arc between their endpoints. It’s like taking a wedge out of the circular pie.
Lastly, a segment is similar to a sector, but it’s the area between an arc and a chord. Imagine cutting across the circle, but not necessarily through the center, and you’ll get a segment.
RESOURCES
These are affiliate links. If you click a link and buy the product, then the blogger gets a percentage of the sale or some other type of compensation. Prices are not different if you use these affiliate links. You will not pay more by clicking through to a link.
RULE 1
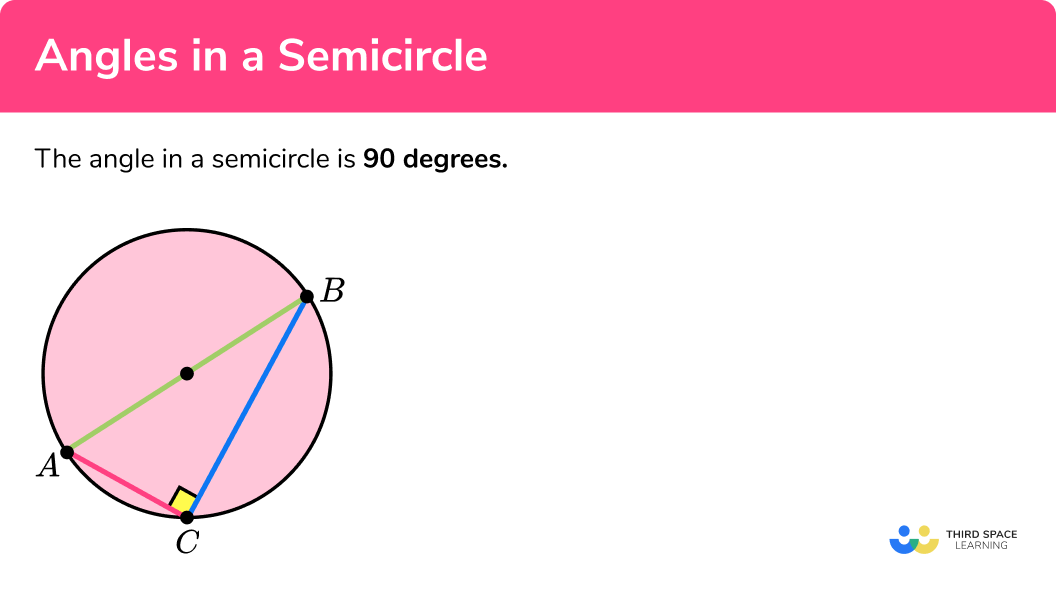
First up is the rule that the angle in a semicircle is always a right angle. So, if you draw a triangle in a circle with one side as the diameter, the opposite angle will always be 90 degrees.
RULE 2
The next theorem states that a tangent to a circle makes a right angle with the radius at the point of tangency. This means if you draw a radius to the point where the tangent touches the circle, they’ll form a 90-degree angle.

RULE 3
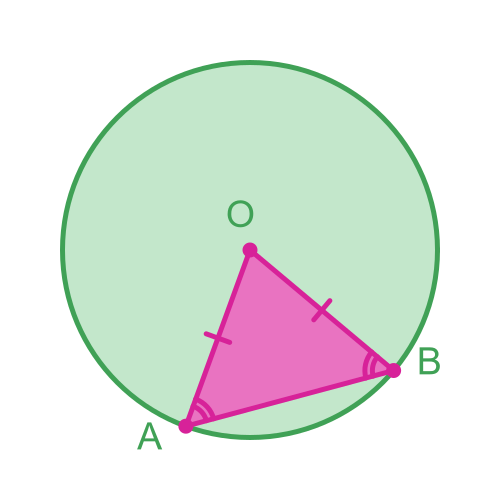
Another important rule is that a triangle formed by two radii is isosceles. Since all radii of a circle are equal in length, any triangle made from two radii of the circle will have at least two equal sides.
RULE 4
The fourth rule tells us that a diameter bisects a chord at right angles. Essentially, if you draw a chord and a diameter intersects it perpendicularly, that diameter will cut the chord into two equal halves.
RULE 5
A more complex theorem involves the angle subtended at the center of a circle, which is double the angle subtended at the circumference by the same arc. This means the angle at the circle’s center is twice any angle on the edge that opens up to the same arc.
RULE 6
Another interesting property is that angles subtended by an arc in the same segment are equal. So two angles that sit on the same arc and segment will match each other.
RULE 7
When dealing with cyclic quadrilaterals—four-sided figures with vertices touching the circle—opposite angles sum to 180 degrees. This can be a handy fact when tackling problems involving cyclic quadrilaterals.
RULE 8
The eighth rule tells us that two tangents drawn from the same point outside a circle are equal in length. This concept helps create congruent right-angled triangles, which are vital in many constructions and proofs.

RULE 9
Lastly, there’s the Alternate Segment Theorem. It explains that the angle between a tangent and a chord is equal to the angle subtended by the ends of the chord in the opposite segment. This theorem is particularly useful in complex geometric proofs.
CONCLUSION
Diving into circle theorems can feel like stepping into a new world, but they’re actually logical once you break them down. These theorems help solve many geometric problems involving circles by providing crucial relationships and properties.



No responses yet