RESOURCES

GCSE Maths AQA Exam Practice Workbook: Foundation – includes Video Solutions and Answers: for the 2025 and 2026 exams (https://amzn.to/4fOfZet)

Edexcel GCSE 9-1 Maths Foundation All-in-One Complete Revision and Practice: Ideal for the 2025 and 2026 exams (Collins GCSE Grade 9-1 Revision) (https://amzn.to/4e4f60g)

GCSE Maths Edexcel 10-Minute Tests – Higher (includes Answers): for the 2025 and 2026 exams (CGP Edexcel GCSE Maths) (https://amzn.to/3W4GCog)

GCSE Maths Edexcel Complete Revision & Practice: Higher inc Online Ed, Videos & Quizzes: for the 2025 and 2026 exams (https://amzn.to/4h4Ud7s)

These are affiliate links. If you click a link and buy the product, then the blogger gets a percentage of the sale or some other type of compensation. Prices are not different if you use these affiliate links. You will not pay more by clicking through to a link.

CALCULATIONS

When dealing with BIDMAS, if there are two or more consecutive divisions and/or multiplications, perform them from left to right. The same applies to addition and subtraction. This might seem straightforward, but it’s a common stumbling block for many.

Adding and subtracting negative numbers can be confusing. Think of adding a negative number as the same as subtracting a positive number. So, when you see a plus sign next to a minus sign, you’d actually subtract. Conversely, subtracting a negative number means you’re effectively adding. So, a minus sign next to another minus sign means you add.

Multiplication and division involving negative numbers follow a simple rule: two numbers with the same sign give a positive result, while two numbers with opposite signs give a negative result. It’s straightforward once you internalize it, but can trip you up if you’re not careful.

MULTIPLES AND FACTORS

Multiples and factors often go hand in hand with arithmetic. Understanding them can simplify a lot of tricky problems. A multiple of a number is the product of that number and any other whole number. For instance, 12 is a multiple of 3 because 3 times 4 equals 12. Common multiples come into play when you’re dealing with two or more numbers. For example, the common multiples of 4 and 6 include 12, 24, and 36 since these numbers can be divided evenly by both 4 and 6.

Factors are the numbers you multiply together to get another number. Factors of 12, for instance, are 1, 2, 3, 4, 6, and 12. A key point here is that common factors divide exactly into two numbers. So, for 12 and 18, the common factors are 1, 2, 3, and 6.

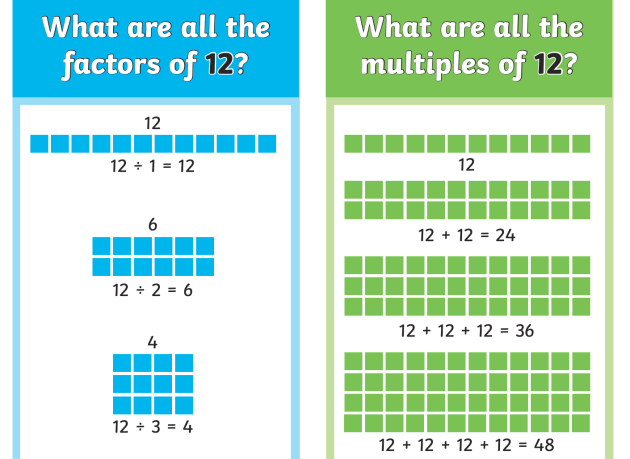
PRIME NUMBERS AND PRIME FACTORS

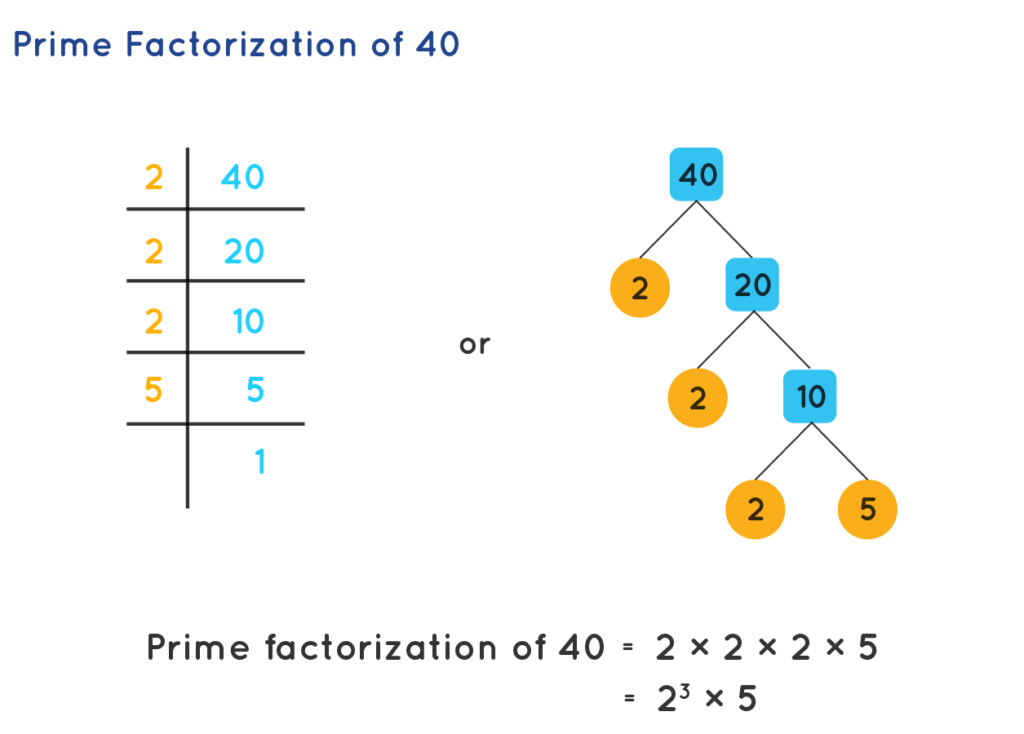
Then there’s the concept of prime numbers—those pesky numbers that aren’t divisible by anything other than 1 and themselves. Examples include 2, 3, 5, 7, and 11. Knowing which numbers are prime can be handy, especially when you need to break down other numbers into smaller components. Any whole number that’s not prime can be broken down into prime factors. Take 12 again: it can be broken down into 2 x 2 x 3, all of which are prime numbers.

LCM AND HCF

Least Common Multiple (LCM) and Highest Common Factor (HCF) are crucial, especially in more advanced arithmetic. The LCM of a set of numbers is the smallest common multiple they share. So, the LCM of 4 and 6 is 12. On the other hand, the HCF is the largest number that divides exactly into two or more numbers—in our case, for 12 and 18, the HCF is 6.

CONCLUSION

Understanding these concepts significantly improves your problem-solving skills. Next time you need to find a common meeting point for numbers, you’ll know exactly how to handle it. Keep practicing these principles in real-life scenarios, like organizing schedules or managing tasks, and they’ll become second nature.