RESOURCES
This is an affiliate link. If you click the link and buy the product, then the blogger gets a percentage of the sale or some other type of compensation. Prices are not different if you use these affiliate links. You will not pay more by clicking through to the link.
ANGLES AND LINES
Angles play a fundamental role in the study of 2D shapes. When you look at angles around a point or on a straight line, they have specific properties. Angles at a point sum up to 360 degrees, while angles on a straight line add up to 180 degrees.
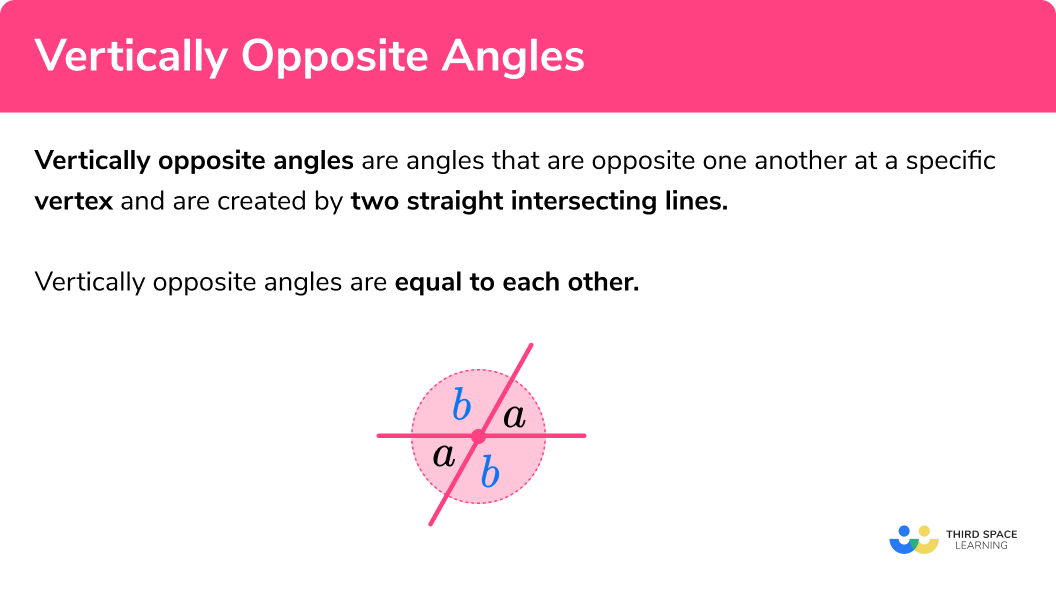
When two straight lines intersect, they form two pairs of vertically opposite angles. These opposite angles are equal. This equality can be helpful when you’re solving problems involving intersecting lines.
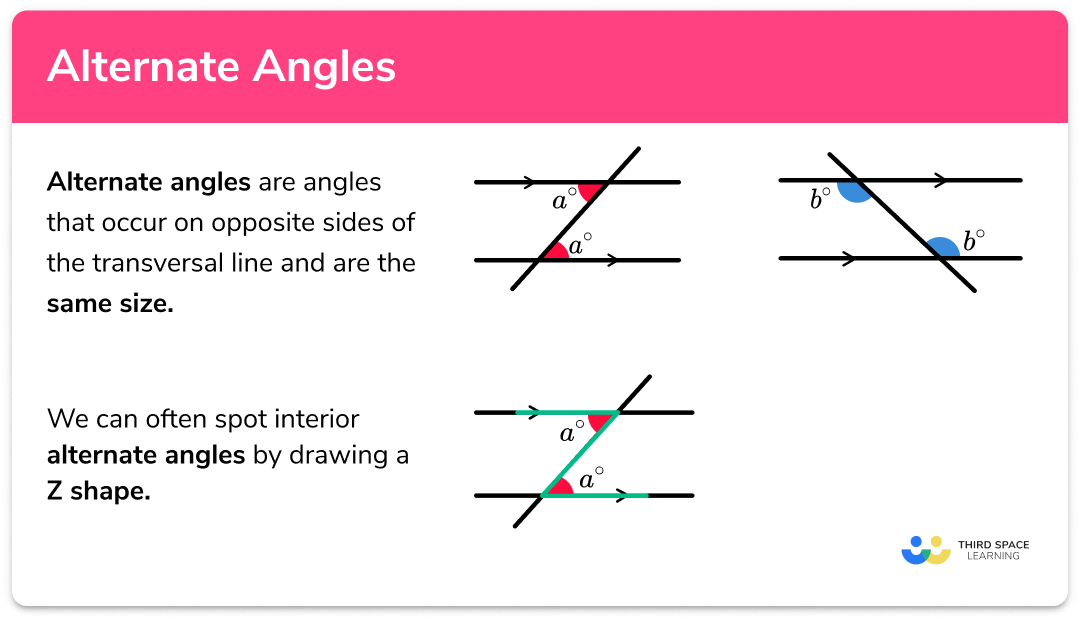
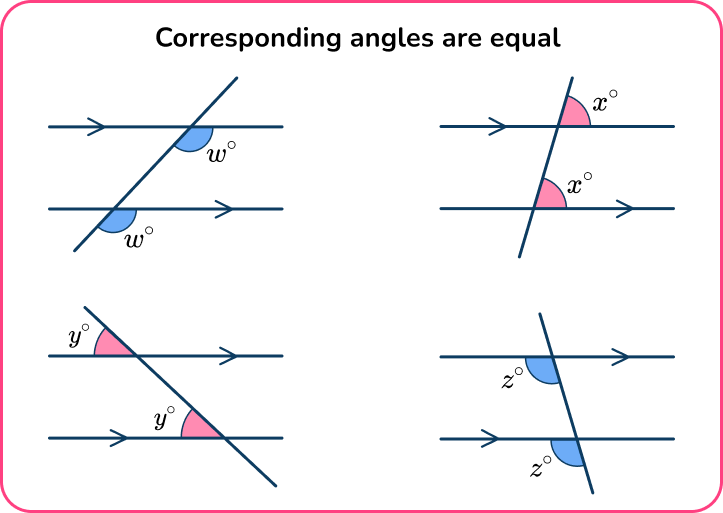
A straight line crossing two parallel lines can create alternate angles, which are equal. This forms a kind of Z-shape and proves useful when working with parallel lines. Similarly, corresponding angles, which form an F-shape, are also equal.
Another useful property is allied angles. When a straight line crosses two parallel lines to form a C-shape, the interior angles on the same side add up to 180 degrees. This can help simplify complex calculations. Understanding these basic properties aids in recognizing shapes and solving geometric problems.


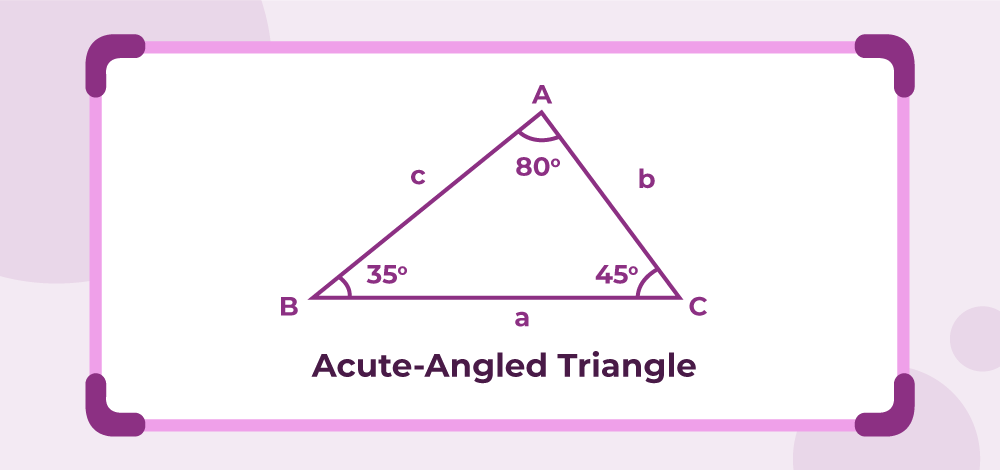
TRIANGLES
Triangles are one of the simplest yet most fascinating shapes in geometry. Each triangle type has unique characteristics that make them special. No matter the type, the sum of a triangle’s interior angles always adds up to 180 degrees.
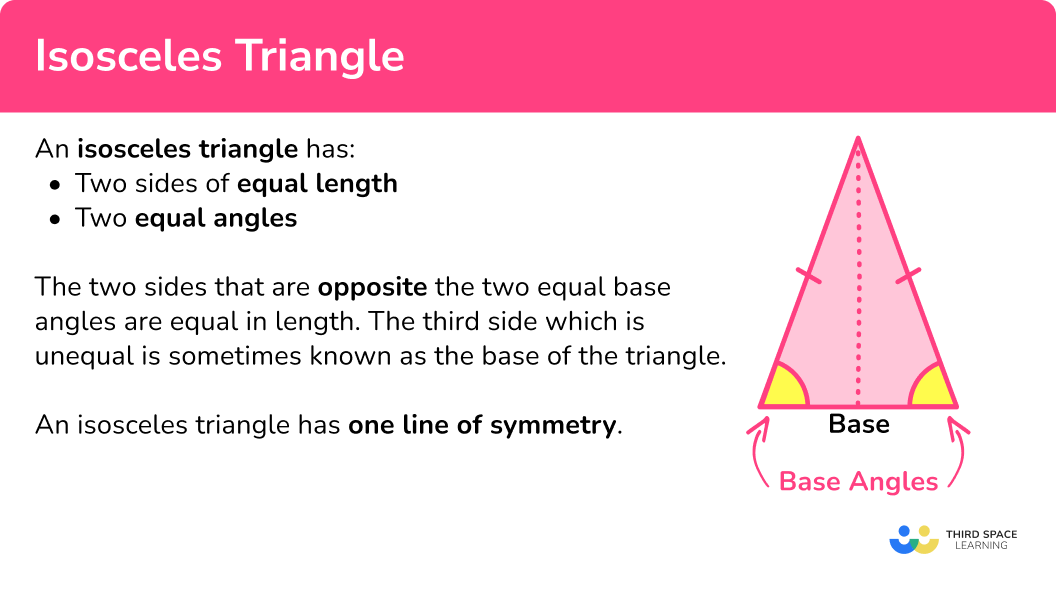
An isosceles triangle has two equal sides and two equal angles. This symmetry can make calculations simpler when dealing with problems involving this type of triangle. Equilateral triangles, which have three equal sides and angles of 60 degrees each, represent perfect symmetry and balance. They’re often used in designs due to their pleasing aesthetics.
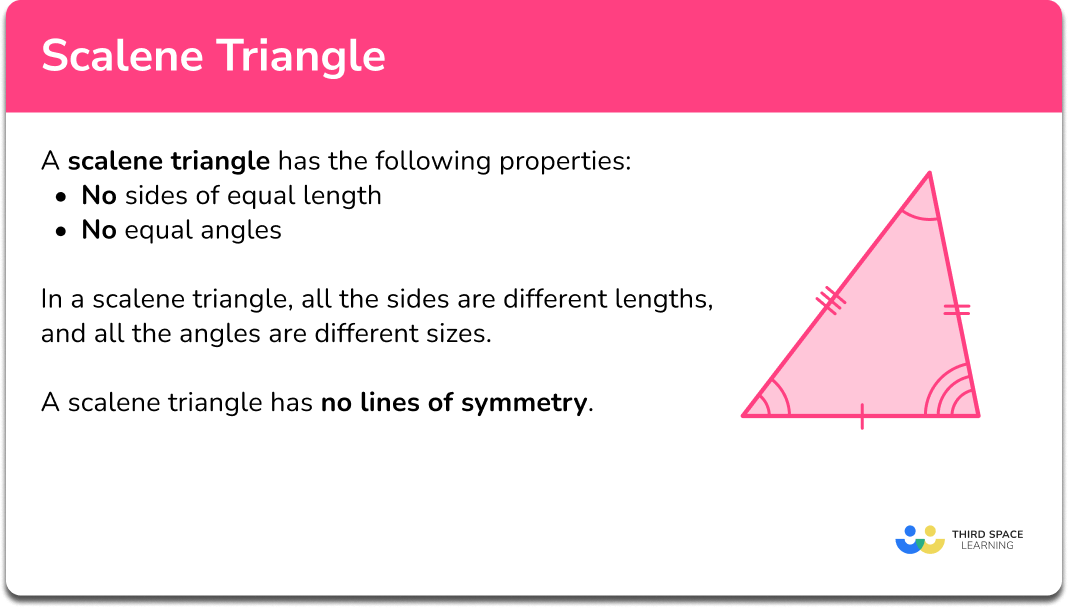
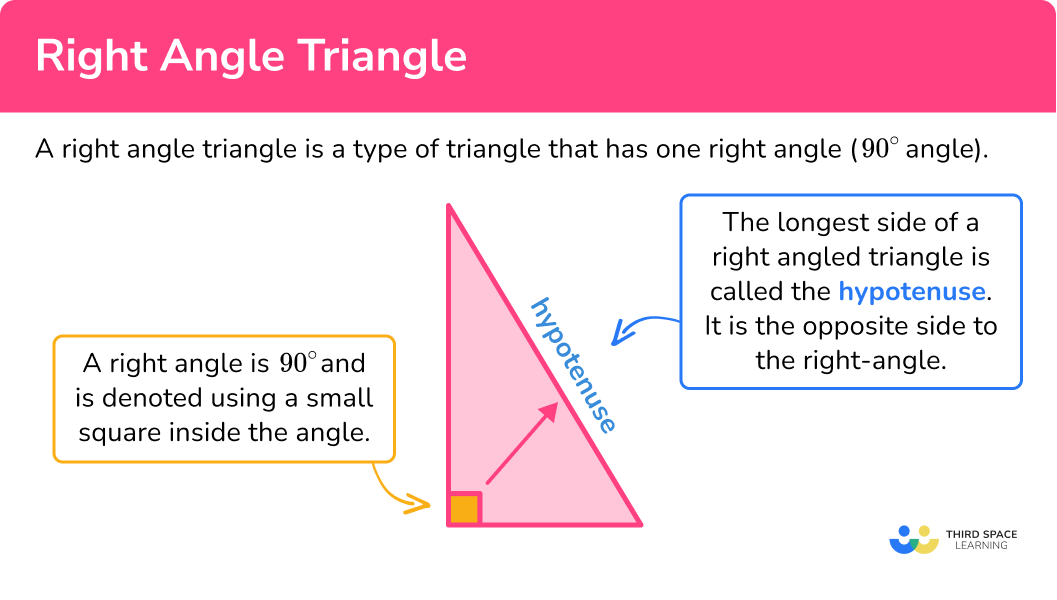
On the other hand, a scalene triangle, with all sides and angles different, provides a more irregular and flexible shape. This variety makes it invaluable in real-world applications where symmetry isn’t always present. Right-angled triangles, with one 90-degree angle, are crucial in trigonometry and various practical fields like construction and engineering.
Acute-angled triangles have three angles each less than 90 degrees, while obtuse-angled triangles have one angle greater than 90 degrees. Recognizing these triangles helps in breaking down complex shapes into manageable segments. Each type offers valuable insights, aiding in problem-solving and practical applications across different fields.

QUADRILATERALS
Quadrilaterals are four-sided shapes with unique properties for each type. The angles in any quadrilateral add up to 360 degrees. Recognizing this can help when working out missing angles or sides in various problems.
A square is a quadrilateral with four equal sides and four right angles. It’s symmetrical and often used in design and architecture for its strong, balanced structure. Rectangles, with four right angles and opposite sides of equal length, offer versatility and practicality in everyday applications.
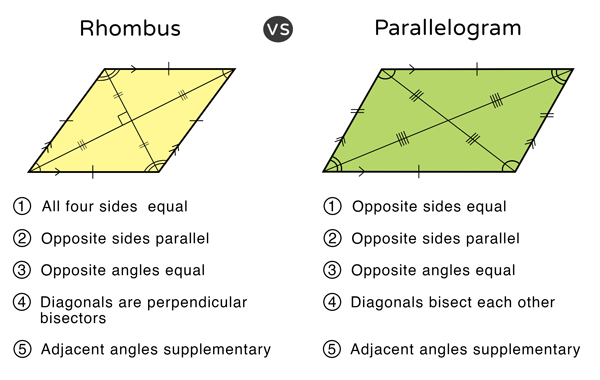
Parallelograms have two pairs of equal, parallel sides. They are more flexible than squares and rectangles but equally important in understanding geometric relationships. Rhombuses, a type of parallelogram with all sides of equal length, showcase the beauty of symmetry in less obvious ways. Their opposite angles are equal, while neighbouring angles sum up to 180 degrees, providing useful properties for solving problems.
Kites feature two pairs of equal sides and one pair of equal angles opposite each other. Their distinct shape proves useful in real-life applications from kite-making to architectural designs. Trapeziums, with only one pair of parallel sides, and isosceles trapeziums, where the non-parallel sides are of equal length, add a layer of complexity and versatility to the family of quadrilaterals.


POLYGONS
Polygons expand the understanding of 2D shapes even further. A polygon’s sides are all straight, and regular polygons boast equal sides and angles. You can calculate the sum of a polygon’s interior angles using the formula: (number of sides – 2) x 180. This approach stems from dividing the polygon into triangles, making it easier to manage.
The exterior angles of any polygon sum up to 360 degrees. Using the exterior angle, you can find the corresponding interior angle with the formula: Interior angle = 180 – Exterior angle. For regular polygons, each exterior angle equals 360 divided by the number of sides, simplifying calculations even more.
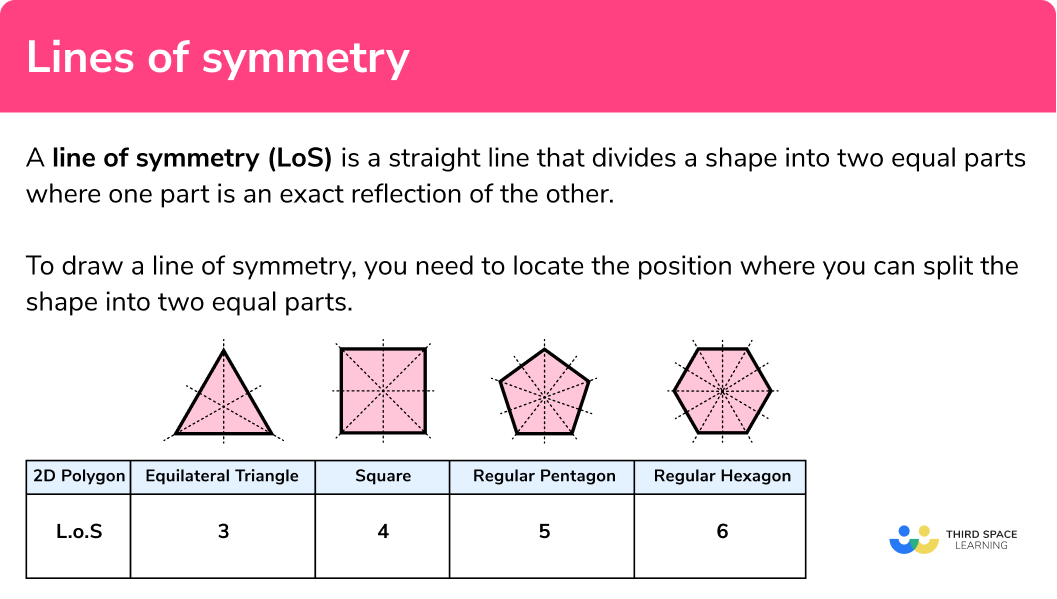
SYMMETRY
Symmetry plays a crucial role in understanding shapes. A shape’s line of symmetry acts as a mirror line, reflecting one side onto the other. Rotational symmetry looks at how many times you can rotate a shape to exactly match its original form. Recognizing these properties aids in both geometric theory and practical applications, from design to problem-solving.



No responses yet