If you’ve ever dealt with algebra, you’ll know expressions are the language of this mathematical domain. But what exactly is an algebraic expression? At its core, an algebraic expression is a combination of numbers, variables, and operations that stands to represent a value. Unlike an equation, an expression is not about finding an ‘answer’; there’s no equal sign demanding resolution.

Expressions are built from terms. Think of a term as a single building block in the larger structure of an expression. It can be as simple as a number or variable, or a product when numbers and variables are multiplied together. For instance, 2x and 3y are terms in the expression 2x + 3y. Here, x and y are ‘variables’, symbols that represent unknown numbers, while 2 and 3 are ‘constants’, the known quantities.

Now, operations are the actions that weave these terms together, including addition, subtraction, multiplication, division, but also extending to exponents and roots. These operations tell us how the terms relate to each after all, an expression is a kind of mathematical narrative.

RESOURCES

• Algebra Evaluating Expressions 100 Worksheets: Practical Exercises for Mastering Algebraic Expression Evaluation in Various Problem Types (https://amzn.to/4h5KZrz)
• Expressions: A Maths Is Not A Mystery TopicBook (https://amzn.to/3DJbPan)

These are affiliate links. If you click a link and buy the product, then the blogger gets a percentage of the sale or some other type of compensation. Prices are not different if you use these affiliate links. You will not pay more by clicking through to a link.

SIMPLIFYING EXPRESSONS

One reason algebraic expressions are so powerful is their capacity for simplification. This is done by ‘collecting like terms’, which means combining terms with the exact same variable parts. Imagine you have 3x + 2x. Since both terms involve the variable x, they can be combined to form 5x. This is simplicity at its best – you’ve just simplified an expression, making it more straightforward for analysis or further calculations.

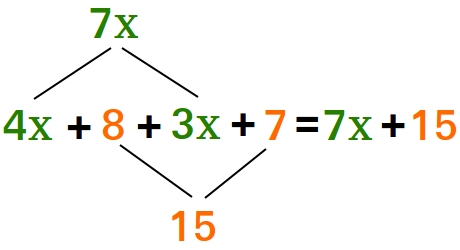
EXPANDING BRACKETS

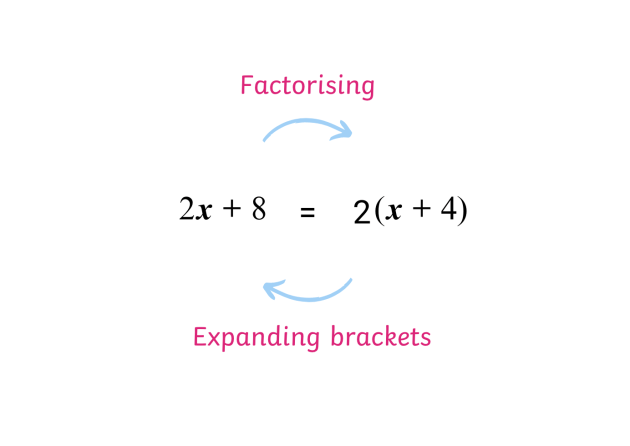
Expanding brackets might have seemed like a tedious task at first, but it is actually the practical application of the distributive property. When faced with an expression like 3(x + 4), it’s essential to multiply every term inside the bracket by the term outside, yielding 3x + 12. This technique simplifies equations and aids in solving more complex algebraic expressions.

FACTORISING WITH COMMON FACTORS

Factorising expressions serves as the reciprocal process, allowing us to look for common factors in an expression and elegantly streamline it into a more manageable form. For instance, taking the expression 15x + 5y, recognizing the common factor of 5 gives us 5(3x + y) as the factorized form.

FACTORISING WITH QUADRATICS

When quadratic expressions come into play, the challenge increases, but so does the intrigue. An expression like x² – 16 may at first seem daunting, yet it hides a simple factorization as the difference of two squares, unravelled as (x – 4)(x + 4). This insight can be the key to unlocking more complicated algebraic equations.

ALGEBRAIC FRACTIONS

As for algebraic fractions, these are expressions that many would rather avoid, but there’s no need for apprehension. By simply factorizing the numerator and denominator and eliminating common factors, we turn an intimidating fraction into something much simpler. Just as you would with numbers, always look to reduce fractions to their lowest terms.

CONCLUSION

Algebraic expressions are not just mathematical puzzles; they represent real-world situations and form the basis for advanced theories and problem-solving across numerous fields. As we delve into the various methods of manipulating these expressions, it’s clear that understanding these techniques is a powerful addition to any problem-solver’s toolkit.

Remember, the goal is to achieve mastery over these concepts for practical use, not just memorizing steps. Mastery will not only benefit academic pursuits but also everyday problem-solving and logical thinking skills. KEEP PRACTICING, stay curious, and you’ll find that algebraic expressions are not just numbers and letters on a page—they’re a language of logic waiting to be decoded.