RESOURCES
This is an affiliate link. If you click the link and buy the product, then the blogger gets a percentage of the sale or some other type of compensation. Prices are not different if you use these affiliate links. You will not pay more by clicking through to the link.
PLANS, ELEVATIONS AND ISOMETRIC DRAWINGS
Plans and elevations are essential for visualizing and interpreting 3D shapes accurately. When tackling 3D objects, it’s crucial to be able to understand how they look from different viewpoints.
The plan is the view you get when looking directly down from above. Imagine you’re a bird soaring above a city—what you see when you look straight down is the plan view. This perspective helps in getting an overall idea of the layout and dimensions, avoiding confusion about what goes where.
Front and side elevations are what you get when you look at an object head-on from the front or side. Think about standing directly in front of a building and sketching what you see; that’s the front elevation. Now, move to the side and repeat; you’ve got the side elevation. Together, these views give a comprehensive understanding of the structure’s form and details.
Isometric drawings add another layer of depth. These are drawn on a special grid where the lines form equilateral triangles, making it easier to represent the 3D structure on a 2D plane. Picture constructing a 3D model on paper without it appearing distorted—that’s what isometric drawings achieve.
These techniques are not just academic exercises. Architects use them to design buildings, while engineers use them to draft mechanical parts. Mastering these skills could open doors to careers in these fields or simply help you in understanding complex everyday objects better.
VOLUME
Getting the hang of volume calculations for different 3D shapes is pretty straightforward once you remember the formulas. Take a cuboid, for example. Its volume is simply the product of its length, width, and height. This comes in handy whether you are packing boxes or figuring out how much space you need for a new piece of furniture.
Understanding prisms can be just as simple. These shapes have a constant cross-section—picture a chocolate bar or a water tank. The volume of a prism is calculated by multiplying the area of its cross-section by its length. Knowing this can be a game changer in practical situations such as determining the capacity of containers.
NETS AND SURFACE AREA
Nets and surface areas are another piece of the puzzle. A net is like a flattened-out blueprint of a 3D shape, showing all its faces. To find the surface area, just add up the areas of these faces. Whether wrapping gifts or crafting models, these skills can come in very useful.
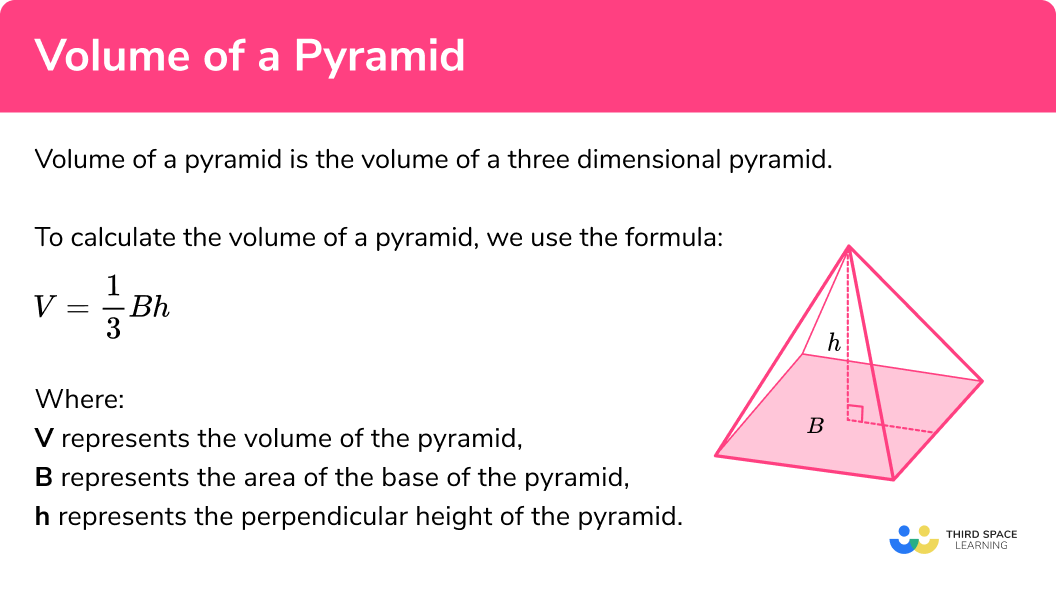
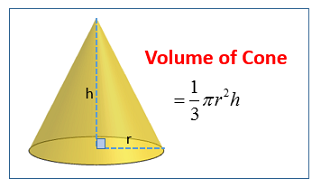
SPHERES, CONES AND PYRAMIDS
When dealing with more complex shapes like spheres, cones, and pyramids, there are specific formulas to keep in mind. A cone’s surface area and volume involve both its radius and height, using π to calculate properly. Pyramids combine the base area and height in their volume formula—perfect for real-life applications like designing roof structures or creating artistic sculptures.


RATES OF FLOW
Rates of flow can often be overlooked, but they play a huge role in daily functions. For example, knowing how much water flows through a pipe per minute can inform decisions in plumbing or irrigation systems. It’s simply the volume divided by time, giving a clear measure of efficiency.

CONCLUSION
Putting these concepts together aids in making informed choices, whether you are a student, a professional, or simply love solving everyday problems. Grasping the volume, surface area, and rates of flow of 3D shapes equips you with practical knowledge essential for various tasks and professions.


No responses yet